Η εξάπλωση της πανδημίας δεν είναι γραμμική. Όμως τα υπάρχοντα προβλεπτικά μοντέλα δεν απαντούν σε ερωτήματα όπως το πώς εμφανίζονται οι νέες παραλλαγές, πώς εξαπλώνονται και πώς εκτοπίζουν τα προηγούμενα στελέχη του κοροναϊού.
Για το λόγο αυτό, ερευνητές από το Μητροπολιτικό Πανεπιστήμιο του Τόκιο πραγματοποίησαν προσομοιώσεις με βάση τη θεωρία των δικτύων που δείχνουν πώς αλλάζουν οι αριθμοί των μολύνσεων σε μια πανδημία όταν εμφανίζεται μια νέα παραλλαγή. Βρήκαν μια μη γραμμική εξάρτηση μεταξύ του πόσο μολυσματική είναι η νέα παραλλαγή σε σύγκριση με την υπάρχουσα, μια επίδραση που δεν είχε παρατηρηθεί νωρίτερα. Το νέο μοντέλο μπορεί να εφαρμοστεί για την κατανόηση πραγματικών πανδημιών όπως του COVID-19 και για την ανανέωση των περιοριστικών μέτρων ελέγχου της πανδημίας. H σχετική μελέτη τους δημοσιεύθηκε στο επιστημονικό περιοδικό Scientific Reports.
Όπως επισημαίνουν οι ερευνητές, από την εξάπλωση του κοροναϊού στα τέλη του 2019, η COVID-19 είχε καταστροφικές επιπτώσεις στις ζωές των ανθρώπων. Με τα απανωτά κύματα των νέων παραλλαγών να συνεχίζουν να εξαπλώνονται σε όλο τον κόσμο, οι επιστήμονες αναζητούν τρόπους για να κατανοήσουν πώς εξαπλώνεται η νόσος. Συγκεκριμένα οι ειδικοί θέτουν ζητήματα όπως το πώς εμφανίζονται νέες παραλλαγές, πώς εξαπλώνονται και πώς καταλήγουν να εκτοπίζουν το υπάρχον στέλεχος. Η κατανόηση της δυναμικής των παραλλαγών στον πληθυσμό χαρακτηρίζονται ως ζωτικής σημασίας για τον έλεγχο της εξάπλωσής τους.
Αποτύπωση
Ένα κλασικό σύστημα αποτύπωσης της δυναμικής της πανδημίας με ένα μοντέλο, είναι το «διαμερισματικό» μοντέλο SIR, που εξετάζει τους αριθμούς των ευπαθών (S), των μολυσμένων (I) και των μελών του πληθυσμού που έχουν αναρρώσει (R).
Τα συγκεκριμένα δεδομένα της πανδημίας συσχετίζονται με εξισώσεις, δίνοντας πολλά από τα κύρια χαρακτηριστικά του τρόπου εξάπλωσης μιας ασθένειας. Η πανδημία εξαπλώνεται πιο γρήγορα πριν την έναρξη της ύφεσης, καθώς μειώνεται ο αριθμός των ευπαθών κρουσμάτων και περισσότεροι ασθενείς αναρρώνουν. Ωστόσο, το μοντέλο δεν μπορεί να εξηγήσει την ποικιλόμορφη φύση του πληθυσμού, καθώς ένα συγκεκριμένο άτομο που έχει μολυνθεί δεν έχει ίση πιθανότητα να μολύνει όλους τους γύρω του, ενώ επιπλέον, ο αριθμός των επαφών που έχουν οι άνθρωποι μπορεί να διαφέρει πολύ από το ένα άτομο στο άλλο. Κάθε μοντέλο που προσπαθεί να καταγράψει τη δυναμική της πανδημίας και να κατανοήσει πού και πώς εξαπλώνεται η νόσος, πρέπει να χρησιμοποιεί ένα πιο εξελιγμένο μοντέλο.
Γι’ αυτό ο ομότιμος καθηγητής Φυσικής Γιουτάκα Οκάμπε και ο καθηγητής Φυσικής Ακίρα Σούντο από το Μητροπολιτικό Πανεπιστήμιο του Τόκιο έχουν στραφεί στη θεωρία των δικτύων, ένα μαθηματικό σύστημα που μπορεί να καταγράφει τον τρόπο με τον οποίο τα μέλη ενός πληθυσμού συνδέονται με άλλους.
Χρησιμοποιώντας διαφορετικούς τύπους δικτύων, μπόρεσαν να δημιουργήσουν ένα πιο ρεαλιστικό μοντέλο για το πώς μπορεί να εξαπλωθεί μια λοιμώδης νόσος. Τα βασικά χαρακτηριστικά περιελάμβαναν καταστάσεις δυναμικής απορρόφησης, καταστάσεις στις οποίες το δίκτυο μπορεί να «κολλήσει» (να παραμείνει στάσιμο) με την πάροδο του χρόνου π.χ. ένα κράτος χωρίς μολυσμένα άτομα. Με λίγες μολύνσεις και χαμηλή μολυσματικότητα, το δίκτυο θα έπεφτε απότομα και πάλι στην κατάσταση χωρίς μόλυνση.
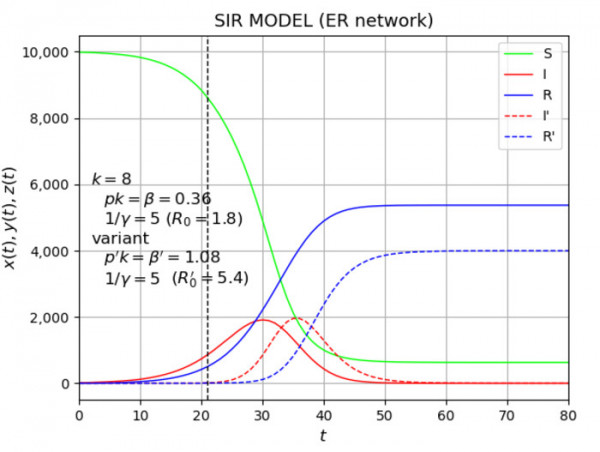
H επίδραση μιας νέας παραλλαγής στην εξάπλωση της πανδημίας (διακεκομμένες γραμμές)
Η ομάδα πραγματοποίησε αριθμητική προσομοίωση ενός μικροσκοπικού μοντέλου στο δίκτυο. Στη μέση μιας προσομοίωσης λοιμώδους νόσου, πρόσθεσαν μια παραλλαγή που είναι πιο μεταδοτική από το αρχικό στέλεχος. Εξετάζοντας τους αριθμούς, η ομάδα διαπίστωσε ότι μια παραλλαγή με την ίδια μολυσματικότητα του υπάρχοντος στελέχους δεν αυξάνεται καθόλου.
Αυτό είναι το άμεσο αποτέλεσμα της μη γραμμικής φύσης της προσομοίωσης, καθώς το δίκτυο «πέφτει» σε κατάσταση «απορρόφησης», όπου δεν υπάρχουν μολύνσεις. Καθώς η μολυσματικότητα της νέας παραλλαγής αυξάνεται, ο πληθυσμός είναι πιο πιθανό να προσβληθεί από την νέα παραλλαγή σε αντίθεση με το υπάρχον στέλεχος, αυξάνοντας το ποσοστό προσβεβλημένων με το νέο στέλεχος σε βάρος του παλιού. Η μη γραμμική φύση του τρόπου με τον οποίο αυξάνονται οι αριθμοί μόλυνσης με την πιο μολυσματική παραλλαγή φαίνεται από τη μικροσκοπική φύση του μοντέλου των δικτύων, δίνοντας μια πιο λεπτομερή, διαφοροποιημένη εικόνα από αυτήν που είχαμε νωρίτερα.
Η ομάδα ελπίζει ότι το μοντέλο της μπορεί να χρησιμοποιηθεί για τη διαμόρφωση αποτελεσματικών στρατηγικών για τον περιορισμό των λοιμωδών νόσων, με την εξέταση των σημείων σημαντικής συνδεσιμότητας εντός του δικτύου και την κατανόηση του πώς η απομόνωση επηρεάζει συνολικά τις λοιμώξεις. Καθώς η πανδημία του COVID-19 συνεχίζει να μαίνεται, βασικές μελέτες για το πώς εξαπλώνονται οι ασθένειες είναι ζωτικής σημασίας για τη λήψη τεκμηριωμένων αποφάσεων με στόχο την επαναφορά της κανονικής ζωής στην κοινωνία.